| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- Convex
- 회귀분석
- pycaret
- 선형회귀
- R
- toolbox
- 머신러닝
- rstudio
- numpy
- MachineLearning
- 데이터사이언스
- normalprobabilityplot
- VSCode
- MATLAB
- Python
- GradientDescent
- LinearRegression
- ~
- Factor
- concave
- 가상환경
- qqplot
- cs229
- Today
- Total
부런의 부지런한 데이터분석
CS229 #1 Part1 ; Gradient Descent, Linear Regression 본문

* 혼자 보고 이해한 내용 적은 거라 틀린 내용 있을 수 있음. 발견 시 댓글 부탁드립니당,,
* 출처 : CS229 notes1 외 google...
- Epoch : one epoch is when an entire dataset is passed forward and backward through the neural network only ONCE
NN에서 전체 데이터셋에 대해 한 번 학습을 완료한 상태(forward랑 backpropagation까지 완료한 걸 하나의 epoch라고 한다)
epoch가 너무 작으면 underfitting / 너무 크면 overfitting
- Batch & iteration
batch 덩어리 / iteration은 반복 횟수라고 보면 되겠다
1 epoch가 모든 데이터셋을 한 번 학습하는 거고 mini-batch는 전체 데이터셋을 batch size로 쪼개서 일부 데이터만으로 학습을 진행하는 것.
ex) 총 데이터가 100개, batch size가 20이라면 100/20= 5번의 iteration. 20개씩 데이터를 뽑아서 5번 반복하면 그게 1 epoch가 되는 것.
우선, 왜 Gradient Descent를 공부하는가? => cost function을 최소화하는 방법에 대해 알아보기 위함이다. 그렇다면 cost function이란 무엇인가? (추가적으로 덧붙이자면 cost function을 최소화하는 parameter를 구해야 하는데, 단순 편미분을 통해 closed-form solution을 구하지 못하는 경우가 존재하기 때문(logistic regression같이). 그럴 때는 일종의 optimization technique이 필요한데, 이 gradient descent가 일종의 최적화 방법이다.)
cost function이란 일종의 error라고 볼 수 있겠다. 우리가 예측한 값에서 실제값을 빼준 것. 즉, 이것을 최소화해야 가장 최적화된 '예측값'을 얻어낼 수 있겠지!

어디선가 언뜻 들었는데 왜 앞에 1/2가 붙냐? 그냥 미분할 때 생기는 2를 없애주기 위함이라고 했음. 아래서 보면 알 수 있듯이 우리는 cost function을 미분하니까! 그 때 계수가 생기면 딱 보기도 더럽잖아 ㅇㅇ
그리고 여기서 h(x)는 hypothesis. linear regression에서는 $\theta^TX$세타 트랜스포즈 엑스. 즉 그냥 내가 알던 linear regression 식이다!
1. Batch Gradient Descent
= minima로 converge할 때까지 파라미터(theta) 업데이트를 반복한다.
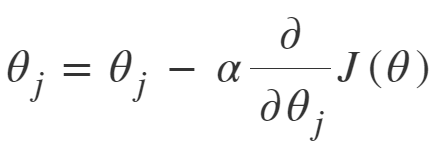
# 편미분해서 나오는 식 다시 한 번 정리하기. $\theta_j$로 미분을 하기 때문에 cost function을 미분하게 되면 속미분 부분에서 x_j만 남게 된다! 그래서 아래 expression1과 같이 x_j가 뒤에 곱해진 형태가 되는 것.
이렇게 생겼으니까 한 번의 파라미터를 업데이트할 때 traning set의 개수만큼 iteration. 왜냐하면 cost function에 $\sum$가 있으니까! 그래서 very large data에서는 very slow한 속도를 보여준다. => computationally expensive
Local minina가 있는 경우에는 취약하지만 linear regression에서는 global optima만 존재하기 때문에 항상 converge to the global minimum.
2. Stochastic Gradient Descent(SGD)
Batch GD에서의 문제점이라면 each step마다 모든 training set을 전부 돌아야 한다는 것. 이러한 문제점을 해결한 방법이라고 할 수 있겠다. Updating the parameters according to the gradient of the error with respect to that single traninig example only. 한 번 파라미터를 업데이트할 때 하나의 training set만 사용해서 업데이트한다.
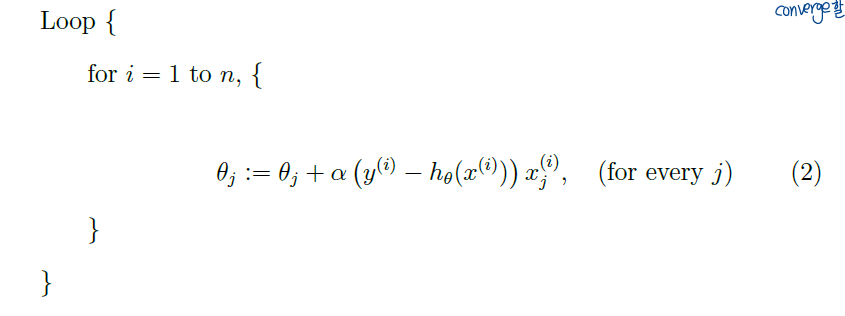

일반적으로 batch GD보다 minimum에 빠르게 도달함. 즉 less computationally expensive하다. 하지만 무조건 converge하지는 않을 수도 있다. minima 근처에서 계속 해서 진동(oscillating하는데 그래도 꽤 합리적인 근사치로 본다). 그래서 이러한 이유로 training set이 크다면 stochastic GD를 batch GD보다 선호한다.
= batch gradient descent has to scan through the entire training set before taking a single step(single step이 한 번 파라미터 업데이트하는 걸 말하는듯),
stochastic gradient descent can start making progress right away, and continues to make progress with each example it looks at. So, particularly when the training set is large, stochastic gradient descent is often preferred over batch gradient descent.
여기까지가 cost function을 최소화하는 방법으로 parameter를 업데이트하는 방법이었다. 'LMS'. Least Mean Square. 즉 LMS는 gradient descent로 parameter를 업데이트하는(찾는) 방법이라고 할 수 있겠다! 하지만 다른 방법도 있지롱
바로바로 The normal equations 되시겠다~ GD같은 경우는 계속해서 반복하는 iterative algorithm이었다. 그렇다보니 시간이 오래 걸리겠지? 그렇다면 반복하지 않고 바로 함으로써 시간을 더 줄이는 게 바로 이것! time performing the minimization explicitly and without resorting to an iterative algorithm, 행렬 사용해주면 한 번에 계산할 수가 있지!

행렬의 미분을 위의 그림처럼 하면 된다는 사실! 사실 별거 없고 그냥 해당하는 A_ij로 각각 미분해주면 그래디언트를 얻을 수 있다.
그럼 다시 cost function J를 최소화해보도록 하자. 근데 이제 iteration 안 할 거니까 matrix-vector notation으로 바꿔줘야 해. 그래서 필요한 개념들.
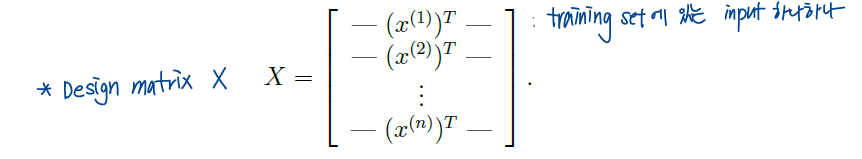
Design matrix X : n X d 형태의 행렬이다. 기본적으로 우리는 column vector를 사용해주기 때문에 transpose를 해준 것. 한 row가 input(training set 중에서 x값) 하나를 얘기한다. 사실은 실제로 쓸 때는 n by d가 아니라 n by (d+1)형태이다. 왜냐하면 우리는 계산을 편하게 해주려고 intercept항을 X에 포함시킬 것이기 때문이지!

여기서 y는 training set에서의 y값이다. 즉 참값과 비슷한 역할을 한다는 것! 파라미터를 이용해 예측한 값이 아니라는 걸 잊지 말자! 결과물은 어떤 값 하나로 딱! 나오니까 행렬의 형태가 아니라 벡터 형태겠지! 차원은 n-dim
우선 차원에 대해 다시 한 번 정리를 하자면, n은 총 training set의 개수이고, d는 feature의 개수이다. target(실제 y값)을 결정짓는 변수들의 개수!
그러면 이제 슝슝슝 과정을 진행해보도록 합시다

앞부분이 우리가 예측한 결과이고 뒷부분이 실제값,, 이라고 하기엔 그런데 참값 역할을 하는 게 되겠지! training set으로 어차피 train하는 거니까,, 이 때 X랑 세타의 순서가 정말 중요하다. 왜냐하면 행렬 계산은 곱하는 순서에 따라서 형태 자체가 달라지니까! 저 두 개를 빼주면 (예측값-참값)들이 행렬로 쫘라락 나오게 된다. 그러면 우리는 이 에러값들을 최소화하는 방향으로 문제를 풀어나가면 되겠지? 에러를 최소화하도록 하자! 그러면 제곱해서 그게 최소화되도록 하면 된다(이전에 단순히 숫자로 했던 과정과 동일). 아니 왜 근데 제곱하나요? 왜냐하면 에러가 음 / 양의 값을 동시에 갖는데 제곱을 안 하면 두 개가 상쇄될 수도 있자낭. 이거는 기본적으로 알고 있다고 보고 진행하지만 나의 미래를 위해 소소하게 기록해놓기,,

행렬에서의 제곱은 제곱하고 싶은 식을 transpose해서 앞에 써주면 된당! 이거는 선형대수 때 했으니까,, 용케 기억한다,,★ 그리고 원래 cost function에 1/2 있으니까 마찬가지로 적어주기! 그러면 이제 무엇을 하면 되냐고요? 뭐하긴 미분하면 되징! 우리는 이 값(에러)을 최소화하는 세타를 찾는 게 목적이니까 세타에 대해서 편미분해주면 된다. derivatives with respect to theta.

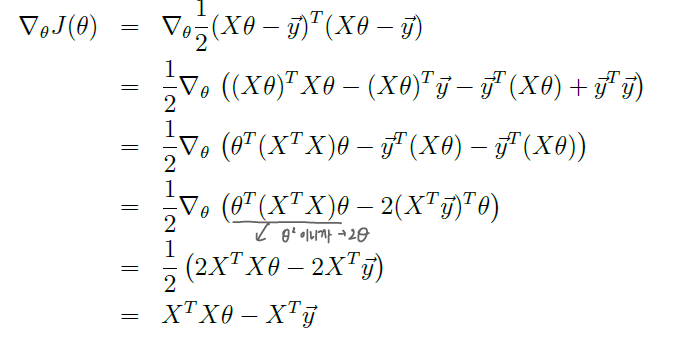
두 번째 줄에서 세 번째 줄로 내려올 때 뒤에 y^Ty가 사라진 이유는 세타가 없으니까 편미분해서 0이 되어서 사라진 것 같다. 행렬은 교환 법칙을 성립하지 않는데 결합 법칙은 성립한다,,, 결합법칙 성립하는 거 맨날 까먹음 좀 기억하도록 하자,,,

결론적으로 cost function을 minimize하려면 저 마지막으로 나오는 게 0이면 된다. 잉? 왜 갑자기 0이냐고? 왜냐하면 minimize라는 건 미분해서 0이 나와야 하니까(max도 마찬가지. optima는 미분해서 0이 나와야하잖아) 그러면 우리는 저 결론으로 나온 식이 0이다. 라는 식을 세워서 세타를 구하면 그 세타가 cost function을 최소화하게 되는 것이다! 그래서 우리는 저거를 normal equations라고 부른다. 저거를 풀면 우리가 원하는 파라미터인 세타를 구할 수 있다는 것이지! 근데 여기서 딱 끝내면 안된다. 왜냐하면 우리의 목적은 세타를 구하는 거니까! '세타 = ' 이런 식으로 바꿔줘야 진짜 모든 과정을 끝냈다고 볼 수 있어! 그러면 남은 건 행렬의 성질 이용해서 이항해주면 끝이다!

이게 cost function J를 최소화하는 파라미터 세타의 값이 되겠습니다~~
근데 차원 한 번 확인해보자! X가 n by d matrix였으니까 앞부분은 d by d 이고 X^T는 d by n 이니까 이거 곱해주면 d by n 이고 y는 n by 1 이니까 전체 차원은 d by 1 형태가 되겠군여! 생각해보면 참 당연합니당 각 변수에 다른 값의 파라미터가 곱해져야 하니까,, 변수 개수만큼 나와줘야져! 근데 위에서도 언급했지만 보다 편한 계산을 위해서라면 d+1 by 1의 차원이 나올 것입니다. 왜냐하면 design matrix X에 intercept항이 하나 더해질 거니까여!
자 이제 그냥 하나하나 보면서 iteration algorithm으로도 해봤고 보다 빠르게 하기 위해 행렬 형태로도 해보았는데요, 과연 이게 reasonable choice일까요? 라고 묻고 있네요. 그래서 이거를 확률적으로 접근해볼 예정입니다... 벌써 끔찍하네요....
제목은 probabilistic interpretation입니다. 확률론적 해석... 사실 이거까지는 안 해도 될 것 같은데... 이거 볼 시간에 다른 걸 보는 게 효율적일 것 같지만 한 번... 도전해보도록 하겠습니다... 근데 보니까 해야할 것 같네요,,, 중도휴학하기 전에 데마 시간에 이거 했던 거네... 교수님 복학해서 다시 열심히 들을게요ㅠㅠ(그리고 작성하는 시점엔 복학해서 수강 중이다)
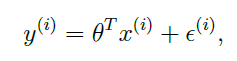

error term은 어떤 값에 의존하거나 영향을 받는 게 아니라 그냥 random한 noise. 평균이 0이고 variance가 sigma square인 정규분포(가우시안 분포)를 따른다고 가정을 하면, error term의 밀도(density)는 저렇게 쓸 수 있다. 저건 그냥 원래 정규분포를 따를 때의 확률밀도함수꼴에 집어넣은 것.
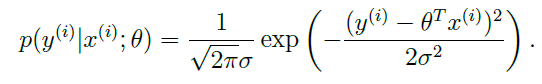
그렇다면 이러한 식이 만족하게 되는데,,, 이 표현에 대한 해석 : x가 주어졌을 때 y값의 확률. 근데 이제 세타에 대해 결정되는... 즉, 우리가 x를 사용해서 y값을 예측하게 되는 거잖아! 그러니까 조건부확률(conditional expectation of Y given x)이 x가 주어지는 거고 그 때의 y값이 되는 거지. 근데 x는 알고 세타는 모르는 값이니까 세타에 대해 결정되는 것! this is the distribution of y given x and parameterized by theta. 여기서 주의해야하는 건 theta는 random variable이 아니라는 것! 그래서 ; 로 나눠서 들어가는 거임.

자 그럼 봐봐. 저 위에서 말한 게 결국 X랑 파라미터 세타가 주어졌을 때 y가 될 확률(분포)이잖아. 그럼 클수록 당연히 좋은 거겠지! 그래서 이거를 설명하려고 새로운 개념을 살짝 도입을 할 건데 그게 뭐냐면 바로바로 Likelihood라는 개념이다!
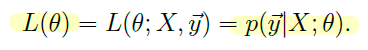
이거를 우리는 Likelihood function이라고 할 것입니다. 한글로는 가능도! 어디선가 퍼온 말에 의하면, 데이터가 특정 분포로부터 만들어졌을 확률이라고 합니다. 데이터가 특정 분포로부터 만들어졌을 확률이니까 그 분포를 잘 따를 확률이라고 봐도 되려나? 웅 맞는 것 같다. 그러면 이 분포를 당연히 잘 따르는 게 좋겠지! 그래서 우리는 이걸 Maximize하도록 할 건데 여기서 잠깐!!!! 바로 위에 있는 식을 조금 더 수식적으로 자세하게 표현해보자.

위에 있는 식은 벡터로 되어 있으니까 하나하나 풀어보면 이렇게 Pi를 사용해줘서 모든 training set에 대한 값을 곱해주면 되겠지 왜냐하면 확률이니까! 그리고 저건 정규분포를 따르니까 (정확히 말하면 error term이 정규분포를 따른다고 가정하고 시작했으니까)(그리고 error term이 I.I.D.니까 걍 다른 거 고려 안하고 그냥 곱하기만 하면 확률이 된다는 것이다!!!) 두 번째 식이 만들어지는 것이고! 이게 likelihood, y가 우리의 분포를 따를 확률이니까 당연히 크면 클수록 좋겠다! 그래서 우리는 maximize likelihood가 되도록 하는 세타를 구할 것이다.
근데 이거 식 봐봐 너무 지저분하잖아 여기서 바로 maximize하면 또 미분하고 그래야하는데,, 파이니까 다 곱해져있어. 생각만 해도 더러워. 그래서 계산을 simpler하게 하기 위해 도입하는 게 있는데요 바로바로 Log likelihood 입니당.

원래 likelihood에 log을 씌워주기만 하면 끝입니다. 그러면 저렇게 식이 정리가 되는데, n은 training set의 개수니까 정해져 있고, sigma도 정해져 있으니까 앞에 있는 term은 무의미해. 그러면 뒤에 값에 의해 log likelihood값이 정해지겠지! 근데 sigma square도 sigma아니까 딱 뒤에 1/2 어쩌구부분에 의해 likelihood값이 결정되게 되는 것! 즉, log likelihood를 최대화하기 위해서는 저 1/2 어쩌구를 minimize하면 된다. 왜냐하면 앞에 마이너스 붙어있으니까!
앗 그러면 보자! 결국 확률론적으로 접근했을 때도 같은 결론이 나왔잖아!(LMS랑 동일) 한 마디로 우리가 그냥 LMS로 해도 합리적인 reasonable한 방법이라는 거지! 그냥 해도 된다는 거야!
+) Note also that, in our previous discussion, our final choice of theta did not depend on what was sigma square => sigma square 값이 unknown이어도 동일한 결과를 도출할 수 있다! 즉 분산의 값에 무관하다.
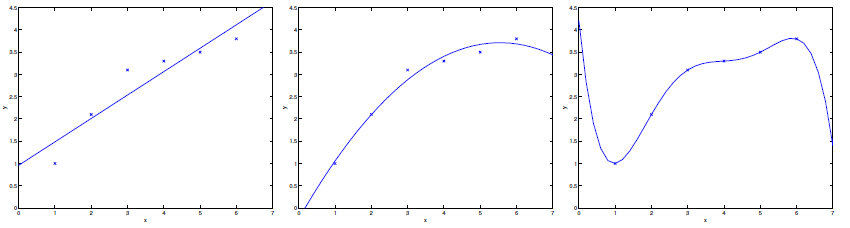
자 여기를 보세요 데이터셋이 파란색 점으로 찍혀있는데요, 우리가 예측할 때 그래프를 이렇게 다양하게 그릴 수 있겠죠? 1번 그림을 보면 경향성이 솔직히 잘 반영이 안 됨. 2번은 딱 적당한 것 같고 3번은 너무 데이터에 심하게 의존하는 것을 볼 수 있습니다. 이럴 때 쓰는 용어가 있죠 바로
1. underfitting : 데이터의 경향성이 너무 반영이 안 되었다는 것이져 - 1번
underfitting같은 경우는 새로운 x가 들어왔을 때 predict의 정확도가 당연히 낮을 수밖에 없으니까 문제입니다. the data clearly shows structure not captured by the model
2. overfitting : 데이터의 경향성이 너무너무 반영이 되었다는 것이져. - 3번
overfitting 같은 경우는 너무 데이터에 의존해서 경향성이 제대로 나오지가 않아요. input값에 너무너무 민감합니다. training set이 변할 때마다 그래프가 슉슉 엄청나게 바뀔 것입니다!
둘 다 안 좋아요 2번이 가장 적합합니당.
한 마디로 모든 feature을 전부 다 동일한 비율로 반영하게 되면 less critical한 것들까지 영향을 많이 줘서 그렇게 유의미한 결과를 얻지 못할 수도 있다는 것. 그래서 feature에 대해 weight를 줌으로써 이를 보정하게 되는데, 이를 우리는 Locally Weighted linear Regression(LWR)라고 합니다. sufficient training data가 있다고 가정하고 LWR에 대해 간단히 알아보도록 합시다.

그냥 Linear Regression이랑 똑같은 과정으로 하는데 달라진 거라면 앞에 weight가 붙은 것밖에 없음! 이 때 weight는 non-negative.

이게 weight를 정하는 standard한 choice인데 자 봅시당. weight가 particular point x에 의존하는 형태. 이 x는 뭐냐면 we're trying to evaluate x(? 정확히 무슨 x를 의미하는지 잘 모르겠다. query point x라고 하는데 x(i)는 training set에 있는 x고 그냥 x는 새로 넣는 x 그러니까 훈련된 모델에 넣는 x값을 의미하는 것 같다는 게 나의 추측임. 근데 맞는 것 같다.)
어쨌든 분자의 절댓값이 작으면 weight는 1에 가까워지고 분자의 절댓값이 크면 weight는 0에 가까워짐. 즉 새로 넣는 x과 training set에 있는 x랑 비슷할수록 가중치를 높게 잡아서 그 영향을 크게 해준다는 거지. 더 잘 반영하도록 한다는 것.
여기서 분모에 있는 타우는 how quickly the weight of a training example falls off를 control하는 요소라고 한다. 'bandwidth parameter'라고 부름
어찌됐든 간단하게 LWR에 대해서도 알아봤는데 이게 그냥 Linear regression과 다른 점을 알아보도록 하자
Non-parametric algorithm / Parametric algorithm
1. parametric algorithm : 관측된 data로 parameter를를 fit해놓으면 이제 training data는 버려도 된다.
ex) (unweighted) Linear Regression : model을 fit해놓으면 이제 새로운 x값만 넣으면 y가 슝 나와버림
2. non-parametric algorithm : model을 fit한 이후에도 training data를 keep해놓아야 한다.
ex) LWR. 모델을 fit해놓아도 또 weight 구할 때 training set 사용하니까 non-para... 인 것 같음
notes1을 다 정리하고 싶었는데 내용이 너무 많아서 새로 작성하도록 해야겠다,,
